Introduction to Arrays in Python: Basic Operations and Applications

In today's digital age, the ability to manage and analyze large amounts of data is critical to business success. Python arrays play a crucial role in this process, allowing companies to perform complex calculations and data analysis efficiently.

That's why we decided to create this article, to offer an introduction to arrays in Python, describing the basic operations and exploring their practical applications in the business world.

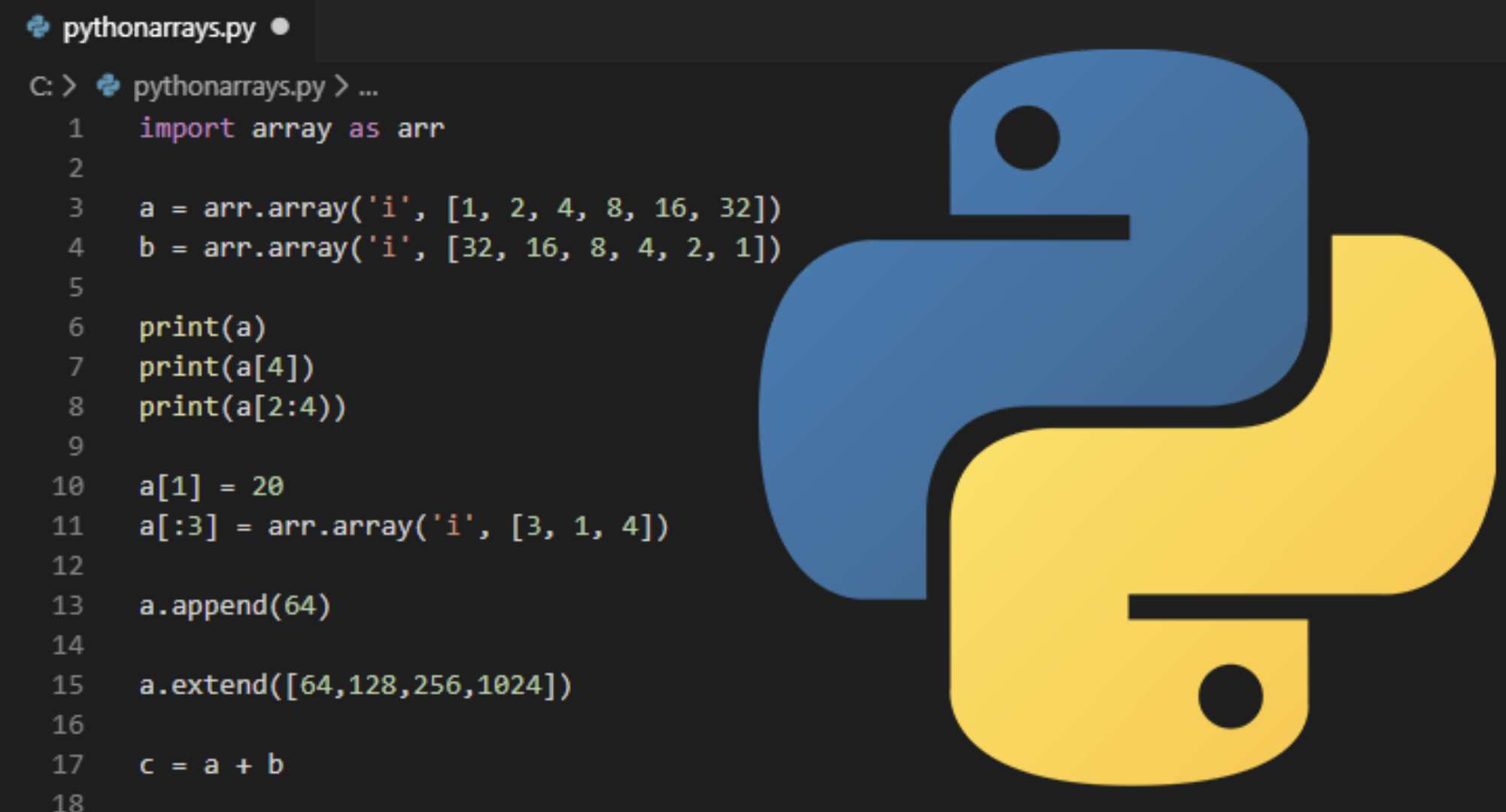
What are Arrays in Python?

Arrays are data structures that store collections of elements, usually numbers, in a two-dimensional format of rows and columns. In Python, arrays are commonly implemented using the NumPy library, which offers a wide range of functions and methods to manipulate this data efficiently.

Installing NumPy

To work with arrays in Python, you must first install the NumPy library. This can be easily done using the following command in your Python terminal or console:

pip install numpy

Array Creation

Once NumPy is installed, you can create arrays using the numpy.array function. Here is a simple example:

import numpy as np

# Creating a 2x3 matrix
matrix = np.array([[1, 2, 3], [4, 5, 6]])

print(matrix)

This code will create a matrix of 2 rows and 3 columns:

[[1 2 3]
 [4 5 6]]

# Creating matrices
matrix_a = np.array([[1, 2], [3, 4]])
matrix_b = np.array([[5, 6], [7, 8]])

# Addition of matrices
sum_matrix = matrix_a + matrix_b

# Subtraction of matrices
diff_matrix = matrix_a - matrix_b

print("Sum:\n", sum_matrix)
print("Difference:\n", diff_matrix)

Sum:
 [[ 6  8]
 [10 12]]

Difference:
 [[-4 -4]
 [-4 -4]]

# Multiplication of matrices
product_matrix = np.dot(matrix_a, matrix_b)

print("Product:\n", product_matrix)

Product:
 [[19 22]
 [43 50]]

# Transposing a matrix
transposed_matrix = matrix_a.T

print("Transposed:\n", transposed_matrix)

Transposed:
 [[1 3]
 [2 4]]

Determinant of a Matrix

The determinant of a matrix is a scalar value that can be calculated using the numpy.linalg.det function.

# Calculating the determinant
determinant = np.linalg.det(matrix_a)

print("Determinant:", determinant)

For the matrix matrix_a, the determinant will be -2.0.

Inverse of a Matrix

The inverse of a matrix is another matrix that, when multiplied by the original, results in the identity matrix. You can calculate the inverse using numpy.linalg.inv.

# Calculating the inverse
inverse_matrix = np.linalg.inv(matrix_a)

print("Inverse:\n", inverse_matrix)

The result of the inverse will be:

Inverse:
 [[-2.   1. ]
 [ 1.5 -0.5]]

Applications of Matrices in Business

Matrices are a powerful tool for various business applications, from data analysis to process optimization. Here are some key areas where matrices can be used to improve efficiency and decision-making in business.

Data Analysis and Modeling

Matrices are fundamental in data analysis, allowing the manipulation and transformation of large datasets. For example, in financial data analysis, matrices can be used to calculate financial indicators, analyze market trends, and predict future behavior.

Moreover, matrices are essential in mathematical and statistical modeling, providing a foundation for linear regression, principal component analysis, and other advanced analysis methods.

Operations Optimization

Matrices are also used in optimizing business operations, helping companies minimize costs and maximize efficiency. For example, matrices can be used to optimize distribution routes, manage inventories, and plan production.

In the logistics sector, matrices are crucial for solving optimization problems, such as the Traveling Salesman Problem (TSP) and Vehicle Routing Problem (VRP), enabling companies to improve their processes and reduce operational costs .

Machine Learning and AI

Machine learning and artificial intelligence heavily rely on matrix operations for data processing and analysis. Machine learning algorithms, such as neural networks, use matrices to represent and manipulate input data, adjust weights, and calculate activation functions.

The ability to handle large datasets and perform complex calculations with matrices is essential for developing accurate and efficient machine learning models, enabling businesses to extract valuable insights and improve decision-making .

Use Case: Sales Prediction

Imagine a company wants to predict future sales based on historical data. Using matrices in Python, the company can apply linear regression techniques to model the relationship between independent variables (factors influencing sales) and the dependent variable (sales).

Here is an example of how matrices can be used to perform this prediction:

from sklearn.linear_model import LinearRegression

# Sample data: [Advertising, Price]
X = np.array([[10, 200], [15, 180], [20, 160], [25, 150], [30, 140]])

# Corresponding sales
y = np.array([300, 400, 500, 550, 600])

# Creating the linear regression model
model = LinearRegression().fit(X, y)

# Predicting future sales
predicted_sales = model.predict(np.array([[35, 130]]))

print("Predicted Sales:", predicted_sales[0])

We recommend you this video